A programming system called LISP (for LISt Processor) has been developed for the IBM 704 computer by the Artificial Intelligence group at M.I.T. The system was designed to facilitate experiments with a proposed system called the Advice Taker, whereby a machine /../ could exhibit “common sense” in carrying out its instructions.
/../
LISP eventually came to be based on a scheme for representing the partial recursive functions of a certain class of symbolic expressions. It now seems expedient to expound the system by starting with the class of expressions called S-expressions and the functions called S-functions.
With that, John McCarthy starts off his Recursive Functions of Symbolic Expressions and Their Computation by Machine paper. Two years after LISP was originally developed, long before many of the concepts presented in the paper become the norm.
Garbage collection, for instance, was first proposed/described in this paper (invented in 1959, paper published in 1960).
While LISP never really delivered on its promise of artificial intelligence and the whole field has started turning in a probabilistic rather than descriptive approach, this paper is a good read for anyone whose interests in computer science and engineering go beyond comparing Ruby to PHP on a syntactical basis.
The Paper is 34 pages long and took me roughly 6 hours to grok, here's the gist in ~1300 words. For details, read the original :)
Functions and function definitions
For starters we need some core mathematical constructs. These are well known, but the conditional expression was believed to be new at the time.
-
Partial Functions - functions only defined on parts of their domain, they arise because the computation is intractable for some values (turing completeness)
-
Propositional Expressions and Predicates - functions/operators returning a true or a false (and, or, not, etc.)
-
Conditional Expressions - a notation for expressing values depending on predicates, which was traditionally done using human words. For instance, definining the function abs(x) benefits from this concept. Best explained with an example:
(1 < 2→4, 1 > 2→3) = 4
(2 < 1→4, 2 > 1→3, 2 > 1→2) = 3
(2 < 1→4,T →3) = 3
(2 < 1→ 0 0,T →3) = 3
(2 < 1→3,T → 0 0) is undefined
(2 < 1→3, 4 < 1→4) is undefined
- Recursive Function Definitions - because of the way conditional expressions are defined, we can use them recursively without falling into infinite loops:
n! = (n = 0→1,T →n · (n−1)!)
2! = (2 = 0→1,T →2 · (2−1)!)
= 2 · 1! = 2 · (1 = 0→1T →·(1−1)!)
= 2 · 1 · 0!
= 2 · 1 · (0 = 0→1,T →0 · (0−1)!)
= 2 · 1 · 1
= 2
The paper also defines propositional operators as recursive functions, because this helps us handle intractability without messing everything up.
p ∧ q = (p→q,T →F)
p ∨ q = (p→T,T →q)
¬p = (p→F,T →T)
p ⊃ q = (p→q,T →T)
- Functions and Forms - the paper makes a distinction between forms - y^2+x - and functions - f(x) = ... - because we need a clean notation for applying functions to parameters. Thus the notion of a lambda is introduced that takes arguments, binds them to an expression and returns the result:
λ((x, y), y^2 + x),
λ((u, v), v^2 + u)
and λ((y, x), x^2 +y)
are the same function
- Expressions and Recursive Functions - lambdas aren't good enough for defining things recursively because you can't have an operator as "the whole expression". To fix this a label is introduced that binds the lambda expression to a name, so it can be reused:
label(sqrt, λ((a, x, eps), (|x2 −a| < eps→x,T →sqrt(a, 1/2(x+ a/x), eps))))
Recursive functions of Symbolic expressions
Now that we have a solid basis, it's time to define symbolic expressions (S-expressions for short), show how they can be used to define functions, how those functions can in turn be represented as S-expressions and finally we will define the all important apply function, which lets the computer calculate anything.
S-expressions are formed by using the special characters dot, left-, right- parentheses [·()] and distinguishable atomic symbols (defined in this paper as capital Latin letters, digits and a single space).
- Atomic symbols are S-expressions
- If e1 and e2 are S-expressions, so is (e1 · e2)
So an S-expression is any ordered pair of S-expressions. Strictly speaking we are supposed to terminate any nesting of S-expressions with a _NIL*, but we agree that (m) stands for (m · NIL) and that instead of a dot operator we can write expressions as lists, which makes our lives a lot easier
((AB,C),D) for ((AB · (C ·NIL)) · (D ·NIL))
((A,B),C,D·E) for ((A· (B ·NIL)) · (C · (D · E)))
Functions of S-expressions use conventional notation, except they're limited to lower case letters, brackets and semicolons to distinguish them from S-expressions. These are called M-expressions (meta-expressions)
car[x]
car[cons[(A· B); x]]
McCarthy then defines five** Elementary S-functions and Predicates**. atom tells us whether something is atomic, eq compares two atomic things and tells us if they're equal, car returns the left part of an S-expression, cdr returns the right and cons constructs an S-expression from two atoms.
By introducing Recursive S-functions we finally get a strong enough class of functions that we can construct all computable functions. McCarthy now defines a bunch of useful functions - let's look at the example of ff, which returns the first element of an S-expression.
ff[x] = [atom[x]→x;T →ff[car[x]]]
ff [((A · B) · C)] = A
calculation:
= [atom[((A · B) · C)]→((A· B) · C);T →ff[car[((A· B)C·)]]]
= [F →((A· B) · C);T →ff[car[((A· B) · C)]]]
= [T →ff[car[((A· B) · C)]]]
= ff[car[((A· B) · C)]]
= ff[(A· B)] = [atom[(A · B)]→(A· B);T →ff[car[(A ·B)]]]
= [F →(A· B);T →ff[car[(A· B)]]]
= [T →ff[car[(A· B)]]]
= ff[car[(A· B)]]
= ff[A]
= [atom[A]→A;T →ff[car[A]]]
= [T →A;T →ff[car[A]]]
= A
The next thing we need is **Representing S-functions as S-expressions. **We do this simply by changing lowercase into uppercase and properly handling some cases around labels and quotes. The M-expression for subst
label [subst; λ [[x; y; z]; [atom [z] → [eq [y; z] → x; T → z]; T → cons [subst [x; y; car [z]]; subst [x; y; cdr [z]]]]]]
becomes the S-expression
(LABEL, SUBST, (LAMBDA, (X, Y, Z), (COND ((ATOM, Z), (COND, (EQ, Y, Z), X), ((QUOTE, T), Z))), ((QUOTE, T), (CONS, (SUBST, X, Y, (CAR Z)), (SUBST, X, Y, (CDR, Z)))))))
Soup. It looks like a soup of weird.
But it's very simple in principle. Add some tactical line breaks and code alignment and you get readable code!
(LABEL, SUBST,
(LAMBDA, (X, Y, Z),
(COND ((ATOM, Z),
(COND, (EQ, Y, Z), X),
((QUOTE, T), Z))),
((QUOTE, T),
(CONS, (SUBST, X, Y, (CAR Z)),
(SUBST, X, Y, (CDR, Z)))))))
The Universal S-Function apply is the all important function that gives us a way of applying a function to a list of arguments. It's a bit tricky to define and reason about - all you have to keep in mind is that it behaves exactly the same as the function it is applying. The main consequence of this is that we can now implement a machine (an interpreter) that only needs to implement the apply function and it can run any program we write.
λ[[x; y]; cons[car[x]; y]][(A,B); (C,D)]
= apply[(LAMBDA, (X,Y ), (CONS, (CAR,X),Y )); ((A,B), (C,D))] = (A,C,D)
In the background, apply is an expression that represents the value of the function applied to arguments, while eval does the heavy lifting of calculation, which takes an expression and its "name" as arguments, so it can attach the value to something useful in the next step of calculation.
And we've come at the juicy goodness of functional programming - **Functions with Functions as Arguments. **The idea is that we can use an S-expression as an argument for another S-expression similar to what we did with apply, except in a more generally useful way.
The paramount example is _maplist _(called "map" these days), which applies a function to every member of a list to construct a different list - for instance increasing all values by +1.
The LISP programming system
LISP's core is a system of translating S-expressions into list structures that can be evaluated by a computer. This system was intended for various uses, the ultimate of which was the Advice Taker system.
Representing S-Expressions by a List Structure can be visualised with a set of connected boxes. Each box is divided into two parts - the right being the address field and the left being the decrement field. They contain the locations for subexpressions returned by car and cdr respectively.
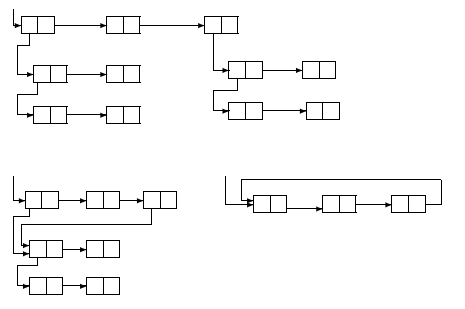
Substructures can be repeated, but cycles aren't allowed - the bottom-right example wouldn't fly. When subexpressions are repeated their in-memory representation depends mostly on the program's history, but luckily this doesn't affect the final result.
The reason McCarthy prohibits circular structures is interesting - they might help with representing, say, recursive functions, but there are too many difficulties with printing them in a world with our topology.
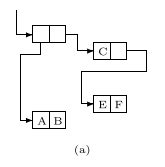
When storing atomic symbols an association list is used. These are used for anything from print names, to memory locations of values - the machine uses them for whatever low-level concept it needs to make the mathematical principles of LISP work.
For example, to store the word DIFFERENTIATE in an association list on a computer with 6-bit words a structure such as this is used:
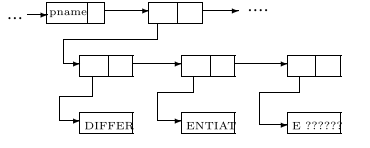
Even back then computers had more memory than a typical program would be using at all times, so a concept of a free storage list was introduced. At its core, the free storage list is simply a list structure that catalogs all the available free memory and starts with a pointer called FREE.
A straightforward concept no doubt, but it introduces the invention of garbage collection. Whenever a subexpression is no longer needed it can be added to the free storage list. And because we're using lists, every single redeemed element is useful!
Sweet!
When our program runs out of free memory the garbage collector (called "a reclamation cycle" back then) goes through all accessible registers and marks them. Then it simply goes through the whole memory and anything that wasn't marked as accessible gets added to the free storage list.
It's easy to imagine how the elementary S-functions work in the Computer. They amount to nothing more than returning the correct part of the word. So _car returns the address value, cdr the decrement value, cons takes from free storage and fills the values ... and so on.
Everything else is merely constructed from elementary functions.
Another interesting observation is that talking about representation of S-functions by Programs McCarthy ever so casually introduces lazy evaluation by saying that compilation is simple and "conditional expressions must be so compiled that only the p's and e's that are required are computed"
There are some problems with compiling recursive functions because of a possibility of register collisions - needing a part of memory that is also used by the previous level of recursion - which is solved by employing a mechanism we now know as The Stack.
Fin
Further on McCarthy details the current state of the LISP system - everything basically works, a manual is being prepared, the compiler is 60-times faster than the interpreter and floating point operations are slow.
There is also a short chapter on an alternative presentation of functions of symbolic expressions called L-expressions. They are the basis of linear LISP and use the more familiar elementary functions first, rest and combine.
Mathematically speaking linear LISP includes LISP, but for computers regular LISP is said to be faster.
Now if only there weren't so many damn parentheses ... I tried to learn LISP (clojure really), I really did. But the syntax was just too jarring.
Continue reading about The birth of LISP - a summary of John McCarthy's original paper
Semantically similar articles hand-picked by GPT-4
- Why people making compilers are superheroes
- Week 1: Turing's On computable numbers
- I learned two things today 29.8.
- Week 15: A tutorial on the expressiveness and universality of fold
- My brain can't handle OOP anymore
Learned something new?
Read more Software Engineering Lessons from Production
I write articles with real insight into the career and skills of a modern software engineer. "Raw and honest from the heart!" as one reader described them. Fueled by lessons learned over 20 years of building production code for side-projects, small businesses, and hyper growth startups. Both successful and not.
Subscribe below 👇
Software Engineering Lessons from Production
Join Swizec's Newsletter and get insightful emails 💌 on mindsets, tactics, and technical skills for your career. Real lessons from building production software. No bullshit.
"Man, love your simple writing! Yours is the only newsletter I open and only blog that I give a fuck to read & scroll till the end. And wow always take away lessons with me. Inspiring! And very relatable. 👌"
Have a burning question that you think I can answer? Hit me up on twitter and I'll do my best.
Who am I and who do I help? I'm Swizec Teller and I turn coders into engineers with "Raw and honest from the heart!" writing. No bullshit. Real insights into the career and skills of a modern software engineer.
Want to become a true senior engineer? Take ownership, have autonomy, and be a force multiplier on your team. The Senior Engineer Mindset ebook can help 👉 swizec.com/senior-mindset. These are the shifts in mindset that unlocked my career.
Curious about Serverless and the modern backend? Check out Serverless Handbook, for frontend engineers 👉 ServerlessHandbook.dev
Want to Stop copy pasting D3 examples and create data visualizations of your own? Learn how to build scalable dataviz React components your whole team can understand with React for Data Visualization
Want to get my best emails on JavaScript, React, Serverless, Fullstack Web, or Indie Hacking? Check out swizec.com/collections
Did someone amazing share this letter with you? Wonderful! You can sign up for my weekly letters for software engineers on their path to greatness, here: swizec.com/blog
Want to brush up on your modern JavaScript syntax? Check out my interactive cheatsheet: es6cheatsheet.com
By the way, just in case no one has told you it yet today: I love and appreciate you for who you are ❤️
