Let's say you have a large piece of text and a dictionary of keywords. How do you quickly locate all the keywords?
Well, there are many ways really, you could even iterate through the whole thing and compare words to keywords. But it turns out that's going to be very slow. At least O(N_keywords * N_words) complexity. Essentially you're making as many passes over the text as your dictionary is big.
In 1975 a couple of IBM researchers - Alfred Aho and Margaret Corasick - discovered an algorithm that can do this in a single pass. The Aho-Corasick string matching algorithm.
I implemented it in Haskell and it takes 0.005s to find 8 different keywords in Oscar Wilde's The Nightingale and The Rose - a 12kb text.
A quick naive keyword search implemented in python takes 0.023s. Not a big difference practically speaking, but imagine a situation with megabytes of text and thousands of words in the dictionary. The authors mention printing out the result as a major bottleneck in their assessment of the algorithm.
Yep, printing.
The Aho-Corasick algorithm
At the core of this algorithm are three functions:
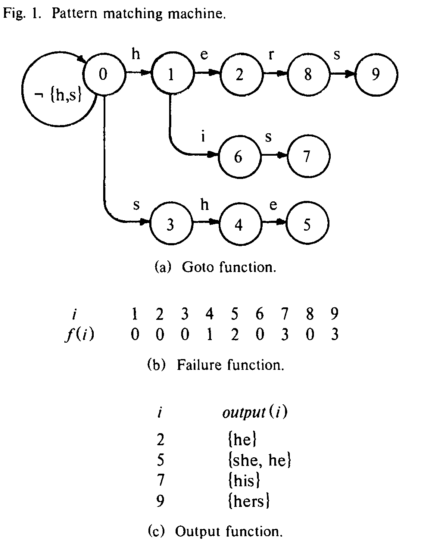
- a parser based on a state machine, which maps (state, char) pairs to states and occasionally emits an output. This is called the Goto function
- a Failure function, which tells the Goto function which state to jump into when the character it just read doesn't match anything
- an Output function, which maps states to outputs - potentially more than one per state
The algorithm works in two stages. It will first construct the Goto, Failure and Output functions. The complexity of this operation hinges solely on the size of our dictionary. Then it iterates over the input text to produce all the matches.
Using state machines for parsing text is a well known trick - the real genius of this algorithm rests in that _Failure _function if you ask me. It makes lateral transitions between states when the algorithm climbs itself into a wall.
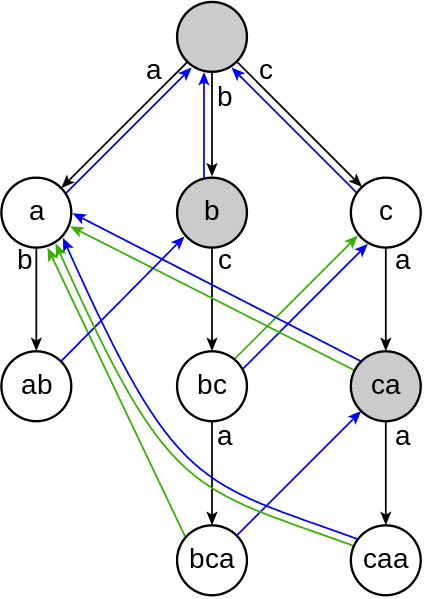
Say you have she and hers in the dictionary.
The Goto machine eats your input string one character at the time. Let's say it's already read sh. The next input is an e so it outputs she and reaches a final state. Next it reads an r, but the state didn't expect any more inputs, so the Failure function puts us on the path towards hers.
This is a bit tricky to explain in text, I suggest you look at the picture from the original article and look at what's happening.
My Haskell implementation
The first implementation I tried, relied on manully mapping inputs to outputs for the Goto, Failure and Output functions by using pattern recognition. Not very pretty, extremely hardcoded, but it worked and was easy to make.
Building the functions dynamically proved a bit trickier.
type Goto = Map (Int, Char) Int
type Failure = Map Int Int
type Output = Map Int [String]
First off, we build the Goto function.
-- builds the goto function
build_goto::Goto -> String -> (Goto, String)
build_goto m s = (add_one 0 m s, s)
-- adds one string to goto function
add_one::Int -> Goto -> [Char] -> Goto
add_one _ m [] = m
add_one state m (c:rest)
| member key m = add_one (fromMaybe 0 $ Map.lookup key m) m rest
| otherwise = add_one max (Map.insert key max m) rest
where key = (state, c)
max = (size m)+1
Essentially this builds a flattened prefix tree in a HashMap of (state, char) pairs mapping to the next state. It makes sure to avoid adding new edges to the three as much as possible.
The reason it's not simply a prefix tree are those lateral transitions; doing them in a tree would require backtracking and repeating of steps, so we haven't achieved anything.
Once we have the Goto function, building the Output is trivial.
-- builds the output function
build_output::(?m::Goto) => [String] -> Output
build_output [] = empty
build_output (s:rest) = Map.insert (fin 0 s)
(List.filter (\x -> elem x dictionary) $ List.tails s) $
build_output rest
-- returns the state in which an input string ends without using failures
fin::(?m::Goto) => Int -> [Char] -> Int
fin state [] = state
fin state (c:rest) = fin next rest
where next = fromMaybe 0 $ Map.lookup (state, c) ?m
We are essentially going over the dictionary, finding the final state for each word and building a hash table mapping final states to their outputs.
Building the Failure function was trickiest, because we need a way to iterate over the depths at which nodes are position in the Goto state machine. But we threw that info away by using a HashMap.
-- tells us which nodes in the goto state machine are at which traversal depth
nodes_at_depths::(?m::Goto) => [[Int]]
nodes_at_depths =
List.map (\i ->
List.filter (>0) $
List.map (\l -> if i < length l then l!!i else -1)
paths)
[0..(maximum $ List.map length paths)-1]
where paths = List.map (path 0) dictionary
We now have a list of lists, that tells us at which depth certain nodes are.
-- builds the failure function
build_fail::(?m::Goto) => [[Int]] -> Int -> Failure
build_fail nodes 0 = fst $
mapAccumL (\f state ->
(Map.insert state 0 f, state))
empty (nodes!!0)
build_fail nodes d = fst $
mapAccumL (\f state ->
(Map.insert state (decide_fail state lower) f, state))
lower (nodes!!d)
where lower = build_fail nodes (d-1)
-- inner step of building the failure function
decide_fail::(?m::Goto) => Int -> Failure -> Int
decide_fail state lower = findWithDefault 0 (s, c) ?m
where (s', c) = key' state $ assocs ?m
s = findWithDefault 0 s' lower
-- gives us the key associated with a certain state (how to get there)
key'::Int -> [((Int, Char), Int)] -> (Int, Char)
key' _ [] = (-1, '_') -- this is ugly, being of Maybe type would be better
key' state ((k, v):rest)
| state == v = k
| otherwise = key' state rest
Here we are going over the list of nodes at depths and deciding what the failure should be for each depth based on the failures of depth-1. At depth zero, all failures go to the zeroth state.
An important part of this process was inverting the Goto HashMap so values point to keys, which is essentially what the key' function does.
Finally, we can use the whole algorithm like this:
main = do
let ?m = fst $ mapAccumL build_goto empty dictionary
let ?f = build_fail nodes_at_depths $ (length $ nodes_at_depths)-1
?out = build_output dictionary
print $ ahocorasick text
A bit more involved than the usual example of Haskell found online, it's still pretty cool :)
You can see the whole code on github here.
Continue reading about Aho-Corasick string matching algorithm in Haskell
Semantically similar articles hand-picked by GPT-4
- Markov chain poem trainer+generator in 29 sloc of Haskell
- Levenshtein distance in Haskell
- Amdahl's law in action - 27s to 0.03s by changing a function
- Haskell and randomness
- Strangest line of python you have ever seen
Learned something new?
Read more Software Engineering Lessons from Production
I write articles with real insight into the career and skills of a modern software engineer. "Raw and honest from the heart!" as one reader described them. Fueled by lessons learned over 20 years of building production code for side-projects, small businesses, and hyper growth startups. Both successful and not.
Subscribe below 👇
Software Engineering Lessons from Production
Join Swizec's Newsletter and get insightful emails 💌 on mindsets, tactics, and technical skills for your career. Real lessons from building production software. No bullshit.
"Man, love your simple writing! Yours is the only newsletter I open and only blog that I give a fuck to read & scroll till the end. And wow always take away lessons with me. Inspiring! And very relatable. 👌"
Have a burning question that you think I can answer? Hit me up on twitter and I'll do my best.
Who am I and who do I help? I'm Swizec Teller and I turn coders into engineers with "Raw and honest from the heart!" writing. No bullshit. Real insights into the career and skills of a modern software engineer.
Want to become a true senior engineer? Take ownership, have autonomy, and be a force multiplier on your team. The Senior Engineer Mindset ebook can help 👉 swizec.com/senior-mindset. These are the shifts in mindset that unlocked my career.
Curious about Serverless and the modern backend? Check out Serverless Handbook, for frontend engineers 👉 ServerlessHandbook.dev
Want to Stop copy pasting D3 examples and create data visualizations of your own? Learn how to build scalable dataviz React components your whole team can understand with React for Data Visualization
Want to get my best emails on JavaScript, React, Serverless, Fullstack Web, or Indie Hacking? Check out swizec.com/collections
Did someone amazing share this letter with you? Wonderful! You can sign up for my weekly letters for software engineers on their path to greatness, here: swizec.com/blog
Want to brush up on your modern JavaScript syntax? Check out my interactive cheatsheet: es6cheatsheet.com
By the way, just in case no one has told you it yet today: I love and appreciate you for who you are ❤️
