Advent of Code Day 20 – Particle Swarm

Day 20 smells like one of those problems that you have to math.

OMG I MADE LEADERBOARD FOR DAY 20!!https://t.co/Jn5odRVtVM #AdventOfCode pic.twitter.com/iDOF1sLREm
— Swizec Teller (@Swizec) December 20, 2017

You're given a large list of particles that each have a velocity vector and an acceleration vector. Velocity tells you where they move and how fast. Acceleration tells you how velocity changes.

You then have to figure out which particle will stay closest to the center – <0,0,0> – in the "long term".

You can math this.

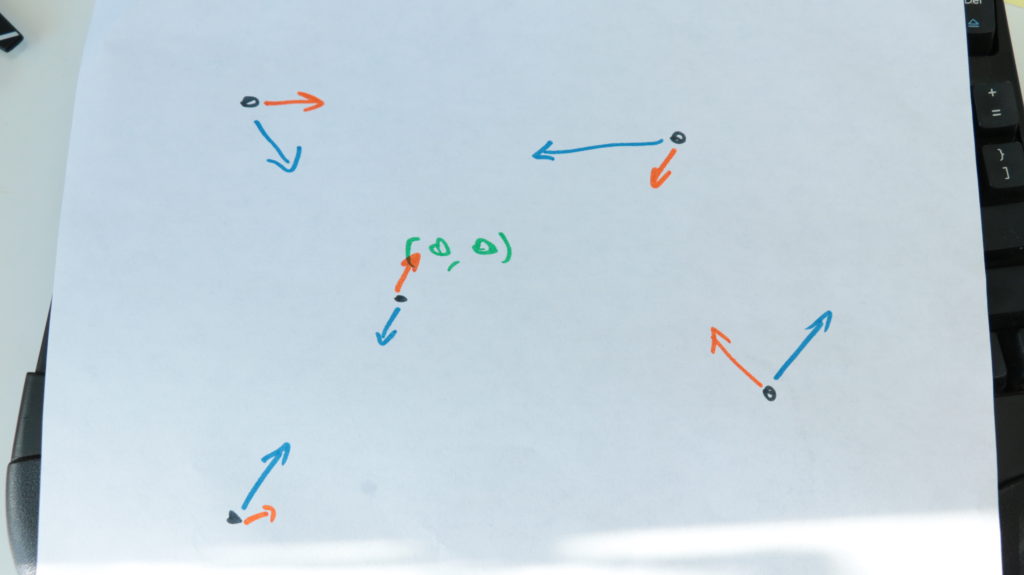
The particle that is accelerating away from center the slowest is the particle that will eventually stay the closest.

This makes sense when you think about it. No matter the initial position or velocity, each particle is either accelerating towards the center, or a way from it. Even if a particle is moving towards the center, it can still be accelerating away from center. Eventually it will fly far far away.

Say a particle starts at p = <3,0,0> and is moving away from center at v = <3,0,0>, but its acceleration is towards center – a = <-1,0,0>. If we iterate through each tick of the simulation, you'll see what I mean 👇

    p = <3,0,0>  v=<3,0,0>  a = <-1,0,0>
    p = <5,0,0>  v=<2,0,0>  a = <-1,0,0>
    p = <6,0,0>  v=<1,0,0>  a = <-1,0,0>
    p = <6,0,0>  v=<0,0,0>  a = <-1,0,0>
    p = <5,0,0>  v=<-1,0,0> a = <-1,0,0>
    p = <3,0,0>  v=<-2,0,0> a = <-1,0,0>
    p = <0,0,0>  v=<-3,0,0> a = <-1,0,0>
    ...

On each tick of the simulation, we add acceleration to velocity, then add velocity to the current position. Our particle that started life flying away from center first slows down, then stops, then hurtles towards center.

After 4 ticks, it reaches center and keeps flying away ever faster.

That's what I mean when by "accelerating away from center". With enough time all particles are accelerating away from center because if they were ever going to cross it, they already have.

But math is hard and modern computers are fast. Even in JavaScript.

Star 1

So we can brute force the solution. No math required 😇

The gist of our bruteforcing is the simulation function itself, the tick. It goes through all particles and moves them.

function tick(particles) {
  return particles.map(({ p, v, a }) => {
    v = v.map((n, i) => n + a[i])
    return {
      p: p.map((n, i) => n + v[i]),
      v: v,
      a: a,
    }
  })
}

That returns a new copy of the particles array with changed positions, p, and velocities, v. Acceleration doesn't change.

We then also need a way to find the particle closest to center. That's these two functions.

function distance(particle) {
  return particle.p.reduce((d, n) => d + Math.abs(n), 0)
}

function closest(particles) {
  return particles.reduce(
    ({ min, index }, p, i) =>
      distance(p) < min
        ? { min: distance(p), index: i }
        : { min: min, index: index },
    { min: distance(particles[0]), index: 0 }
  )
}

distance gives us the Manhattan distance between the center and a particle. closest finds the particle with the smallest distance and returns its index and distance min.

Then we just run the simulation until the closest particle doesn't change for a while. I got good results with "hasn't changed in 2000 ticks". Some fiddling required.

Generally the larger that number, the more accurate your result. If you describe the problem in terms of search algorithms (you're searching for a stable state), then any sequence of stable states when the min distance doesn't change for a while is a local maximum. You're looking for the global maximum.

The longer you keep looking, the likelier that you're at the best possible result.

function star1(input) {
  let particles = prepInput(input)

  let stable = {
    min: 0,
    index: 0,
    iterations_unchanged: 0,
  }

  while (stable.iterations_unchanged < 2000) {
    particles = tick(particles)

    const { min, index } = closest(particles)

    if (stable.index === index) {
      stable.iterations_unchanged += 1
    } else {
      stable.min = min
      stable.index = index
      stable.iterations_unchanged = 0
    }
  }

  console.log(stable)
}

Keep track of the result and how long it's remained unchanged. Repeat until desired accuracy.

Runs in about a second on my machine. 👌

Star 2

Star 2 really stretched what I thought was possible with JavaScript: Finding collisions.

When particles overlap, they are removed from the pool. Your goal is to find how many particles are left standing after "long enough".

The question can once gain be translated into "What's the steady state?".

But how do you find colliding particles?

The simplest approach is to compare every particle with every particle. Surprisingly, that's good enough. Modern computers are fast.

Collision detection is a huge field of algorithmics, by the way. It is definitely not supposed to be as easy as comparing every particle with every particle.

function collision(particles) {
  return particles.map((particle, idx) => {
    const {
      p: [x, y, z],
    } = particle

    if (
      particles.find(
        ({ p }, i) => i !== idx && p[0] == x && p[1] == y && p[2] == z
      )
    ) {
      particle.dead = true
    }
    return particle
  })
}

Returns a new copy of the particles array with every particle for which a particle exists in the same position marked as dead.

To run the experiment, we then use a similar setup as before 👇

function star2(input) {
  let particles = prepInput(input)

  let stable = {
    length: particles.length,
    iterations_unchanged: 0,
  }

  while (stable.iterations_unchanged < 2000) {
    particles = collision(tick(particles)).filter(({ dead }) => !dead)

    if (stable.length === particles.length) {
      stable.iterations_unchanged += 1
    } else {
      stable.length = particles.length
      stable.iterations_unchanged = 0
    }
  }

  console.log(stable)
}

Keep track of stable state and how long it's been stable for. Run the tick simulation, detection collision, and filter dead particles.

After a few seconds, the result pops out.

Paying $3,000 for a laptop was very worth it 👌

Published on December 20th, 2017 in Front End, Technical

Did you enjoy this article?

👎👍

Continue reading about Advent of Code Day 20 – Particle Swarm

Semantically similar articles hand-picked by GPT-4

Senior Mindset Book

Get promoted, earn a bigger salary, work for top companies

Learn more

Have a burning question that you think I can answer? Hit me up on twitter and I'll do my best.

Who am I and who do I help? I'm Swizec Teller and I turn coders into engineers with "Raw and honest from the heart!" writing. No bullshit. Real insights into the career and skills of a modern software engineer.

Want to become a true senior engineer? Take ownership, have autonomy, and be a force multiplier on your team. The Senior Engineer Mindset ebook can help 👉 swizec.com/senior-mindset. These are the shifts in mindset that unlocked my career.

Curious about Serverless and the modern backend? Check out Serverless Handbook, for frontend engineers 👉 ServerlessHandbook.dev

Want to Stop copy pasting D3 examples and create data visualizations of your own? Learn how to build scalable dataviz React components your whole team can understand with React for Data Visualization

Want to get my best emails on JavaScript, React, Serverless, Fullstack Web, or Indie Hacking? Check out swizec.com/collections

Did someone amazing share this letter with you? Wonderful! You can sign up for my weekly letters for software engineers on their path to greatness, here: swizec.com/blog

Want to brush up on your modern JavaScript syntax? Check out my interactive cheatsheet: es6cheatsheet.com

By the way, just in case no one has told you it yet today: I love and appreciate you for who you are ❤️

Senior Mindset Book

Start with a free chapter

Advent of Code Day 20 – Particle Swarm

Star 1

Star 2

Did you enjoy this article?

Continue reading about Advent of Code Day 20 – Particle Swarm

Learned something new?
Read more Software Engineering Lessons from Production

Software Engineering Lessons from Production

Senior Mindset Book